Example 1 of Pajek-XXL usage

For demonstration purposes we will use dictionary network dic28.net. This network represents connections among English words in a dictionary. It was generated from Knuth's dictionary. Two words are connected by an edge if we can reach one from the other by
- changing a single character (e. g., work - word)
- adding / removing a single character (e. g., ever - fever).
There exist 52,652 words (vertices in a network) having 2 up to 8 characters in the dictionary. The obtained network has 89038 edges.

Although the typical use of Pajek-XXL will be demonstrated on a relatively small network, that can be handled with Pajek as well, the same steps can be performed on networks with some 100's of millions of vertices as well.

  1. Load dic28.net to Pajek-XXL.
    When read in Pajek-XXL vertices are described with sequential numbers (1-52652) only.
    Vertex-ID drop-down menu is empty - vertex IDs are equal to vertex numbers (v1-v52652).

  2. In Pajek-XXL compute weakly connected components of the network (Network / Create Partition / Components / Weak). After obtaining partition as a result, sort clusters in the partition in decreasing order according to frequencies (Partition / Canonical Partition / with Decreasing Frequencies). In this way Partition / Info gives us a more clear overview of the sizes of components: 
    Cluster  Freq   Freq% CumFreq CumFreq% Represent
------------------------------------------------
      1 24831 47.1606   24831  47.1606         2
      2  1125  2.1367   25956  49.2973     20602
      3    27  0.0513   25983  49.3486     15043
      4    26  0.0494   26009  49.3979      3556
      5    25  0.0475   26034  49.4454     34848
      6    23  0.0437   26057  49.4891     11480
      7    22  0.0418   26079  49.5309     10573
      8    21  0.0399   26100  49.5708     14940
      9    19  0.0361   26119  49.6069     11232
     10    19  0.0361   26138  49.6429     14378
     11    19  0.0361   26157  49.6790     25644
     12    18  0.0342   26175  49.7132     10235
     13    18  0.0342   26193  49.7474     16737
     14    17  0.0323   26210  49.7797     11825
     15    17  0.0323   26227  49.8120     12531
     16    16  0.0304   26243  49.8424     25130
     17    15  0.0285   26258  49.8709      9893
     18    15  0.0285   26273  49.8993     24931
     19    15  0.0285   26288  49.9278     12486
     20    15  0.0285   26303  49.9563     12235
     ...
    Now you can extract and analyse separately the largest component (which is now - when components are sorted in decreasing order - the first one). The size of the largest component is less than 50% of the size of the original network.
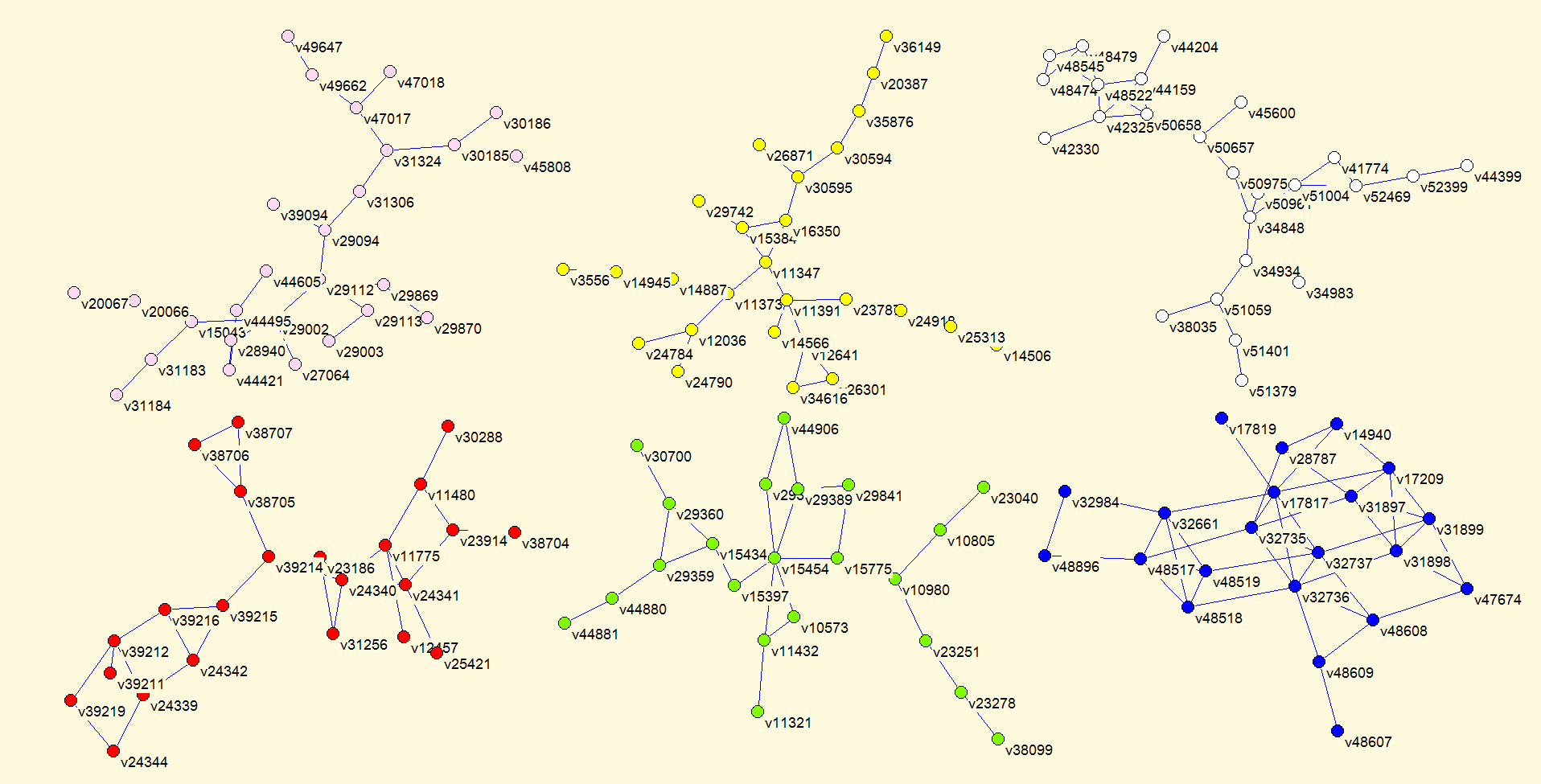
    Or, you can select and visualize some smaller components. Lets extract components 3-8 (with sizes from 27 down to 21 vertices).
    Run Operations / Network+Partition / Extract SubNetwork and select 3-8 in the dialog box.
    (In case that you would work with a huge network you would get additional question Create a new Network as a result? If the old network is not needed anymore answer No is recommended to free a lot of memory space.)
    The obtained extracted network has 144 vertices, which are renumbered to 1-144 again. To identify them we get the following values in Vertex-ID pop-down menu (double click VertexID drop down menu to see): 
      1.   3556
  2.  10573
  3.  10805
  4.  10980
  5.  11321
  6.  11347
  7.  11373
  8.  11391
  9.  11432
 10.  11480
...
142.  51401
143.  52399
144.  52469
    Explanation: Vertex with number 1 is vertex v3556 in dic28.net, vertex with number 2 is vertex v10573, etc.

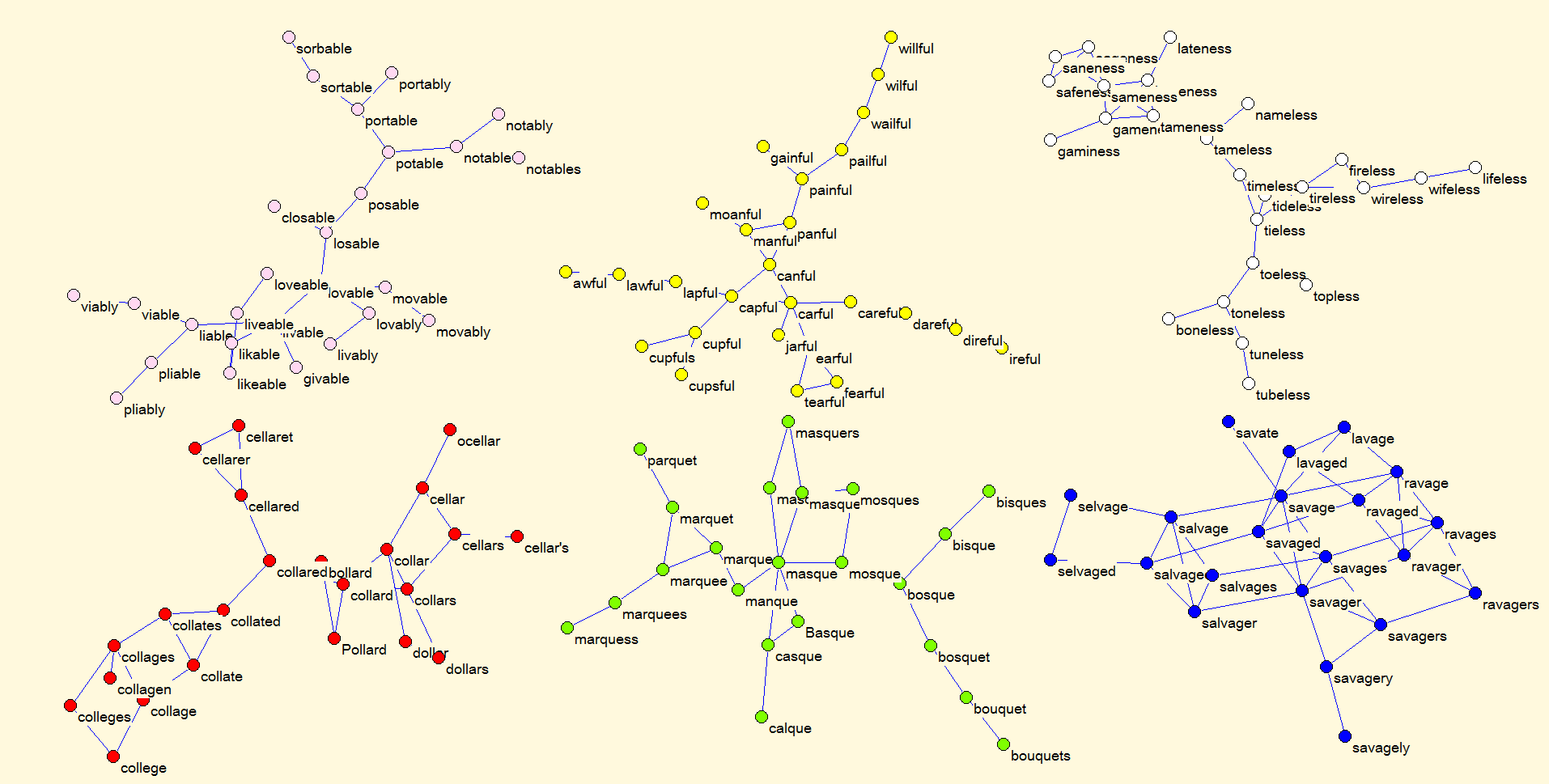
Now you can use Option 1 or Option 2 to bring extracted subnetwork from Pajek-XXL to Pajek.

Option 1:
You can call program Pajek directly from Pajek-XXL with the extracted network where labels are replaced with the right ones (stored in the file). For that purpose use the command: Tools / Pajek / Send Network to Pajek / +Add Vertex Labels from File(s).

Option 2:
If you for some reason do not want to call Pajek directly from Pajek-XXL (maybe not enough memory is available to have Pajek-XXL and Pajek running at the same time), you can save the obtained subnetwork first, later call Pajek, load the network and replace labels with the real ones. Sequence of steps to do this is the following one:
  1. By saving the network in a usual way to a NET file, you get network with labels v3556, v10573,...,v52469. Be sure that Options / Read-Write / Save VertexIDs as Vertex Labels? is checked before saving (otherwise definition of vertices is not written to a NET file). 
    *Vertices 144
1 v3556
2 v10573
3 v10805
4 v10980
5 v11321
...
142 v51401
143 v52399
144 v52469
*Edges
1 19 1
2 9 1
2 24 1
3 4 1
3 33 1
4 25 1
...

  2. Now run 'ordinary' Pajek, load the saved network with 144 vertices and run weakly connected components again.
    You can draw the network with Layout / Energy / Kamada-Kawai / Separate Components and obtain the layout with labels v3556, v10573, v10805,...,v52469:

  3. Run Network / Create New Network / Transform / Add/Vertex Labels / from File(s) and select file with labels (dic28.net). Finally, the obtained network has the original labels: awful, Basque, bisque,..., wifeless, wireless. If you draw this network you get:

By saving the obtained network in a usual way to a NET file, you get a NET file with additional information (labels, coordinates): 

*Vertices 144
1 "awful"          0.4051  0.0491  0.5000
2 "Basque"         0.5323  0.7016  0.5000
3 "bisque"         0.4669  0.8832  0.5000
4 "bosque"         0.4743  0.8199  0.5000
5 "calque"         0.4921  0.6524  0.5000
...
142 "tuneless"     0.7075  0.2723  0.5000
143 "wifeless"     0.8587  0.1067  0.5000
144 "wireless"     0.8508  0.1668  0.5000
*Edges
  2   3 1
  3   4 1
  1   3 1
...
Next example

About Pajek-XXL; Download Pajek-XXL.